преимущества, недостатки, какие мышцы работают и инструкция по эксплуатации (85 фото)
Большинство горожан в настоящее время уделяет особое внимание своему здоровью и, как следствие, тенденция к здоровому образу жизни за последнее десятилетие существенно возросла. Люди следят за качеством и количеством съеденных продуктов, занимаются спортом и просто активным отдыхом.

Многие стремятся поддерживать свою форму не посещая спортзалы и дорогостоящие занятия и, при этом, не отрываясь от домашних дел или любимых фильмов.

Отличным решением в данном случае является приобретение тренажера для дома, на котором можно прорабатывать все группы мышц. Как вы уже догадались, речь пойдет об эллипсе.

Содержимое обзора:
Описание
Эллиптический тренажер – это наиболее подходящий вариант для домашних тренировок. Эллипс является основным тренажером для тренировки сердца. Специалисты утверждают, что при занятии на таком тренажере отсутствует нагрузка на суставы, поэтому негативное воздействие на опорно-двигательный аппарат полностью исключено.
Эллипс – это отличный выбор для людей любого возраста, в том числе и пожилого. Занятия на эллиптическом тренажере по своему принципу похожи на ходьбу на лыжах, а стандартные программ тренировок позволяют выбрать подходящий темп и нагрузку так, что занятия будут приносить удовольствие и положительный результат.

Эллиптическая ходьба способствует уменьшения жировой прослойки и набору мышечной массы тела благодаря нагрузке на проблемные участки тела.

Такие устройства очень популярны в настоящее время и ни один фитнес-зал не обходится без эллипса. Итак, на что же следует обратить внимание при покупке спортивного тренажера для дома?

Вес и размер
Если верить тренерам и спортсменам, то такой агрегат должен быть достаточно массивным и по весу, и по размеру. Это и к маховику тоже относится.

Чем он больше и тяжелее, тем комфортнее и мягче ход тренажера и больше выбор программ нагрузки. На устойчивость агрегата также влияет его вес.
Вид тренажера
Существует всего несколько разновидностей данного тренажера и различаются они способом регулировки нагрузки:

Магнитный эллипс – это лучший тренажер для дома. Программы задаются при помощи панели управления, а регулировка происходит под магнитным воздействием. Единственный минус этой модели заключается в отсутствии профессиональных программ.

Аэромагнитный эллипс. Принцип действия его схож с предыдущим, но механизм имеет систему охлаждения, что позволяет проводить на нем длительные и высоко эффективные тренировки.

Электромагнитный эллипс – это современный, усовершенствованный вариант эллиптического тренажера. Нагрузка регулируется при помощи электромагнитов.

Такая система регулировки позволяет очень точно контролировать нагрузку. Минусами такой разновидности эллипса является его высокая стоимость и необходимость подключения к сети.
Длина шага
Высокая эффективность и результат тренировки зависит именно от длины хода тренажера. Также этот фактор влияет на безопасность его использования. Длина шага может быть зафиксированной (у более бюджетных вариантов) или настраиваемой.

Ограничения по максимальному весу
У многих тренажеров, разработанных для домашних занятий этот показатель обычно составляет от 100 до 190 килограмм. Если вы хотите, чтобы эллипс прослужил вам длительное время, то максимально допустимый вес должен быть на 10-15 килограмм больше вашего исходного.

Программы и настройки
На эту функцию следует обращать внимание исходя из цели приобретения гребного тренажера для дома. Хотите ли вы похудеть, подкачать мышцы или заниматься с целью общего оздоровления организма.

Стандартный набор программ содержит 4-5 вариантов тренировок и как минимум 5 счетчиков: расстояния, скорости, калорий и пульса.

Качество тренажера и набор функций напрямую зависит от стоимости тренажера, чем он дороже, тем больше его функционал. Изучив данную статью, вы будете точно знать какой тренажер выбрать для дома.

Фото эллиптического тренажера для дома






































Также рекомендуем просмотреть:
Тренажер эллипсоид: фото и цены
Итак, вы видите на картинке тренажер эллипсоид. В последнее время данный кардиотренажер приобрел широкую популярность среди любителей спорта и людей, желающих похудеть. Главной особенностью этого устройства можно назвать его универсальность, так как он способен заменить велотренажер, беговую дорожку и степпер.
Есть люди, которые выбирают эллипсоидный тренажер по фото, однако спешим вас заверить, что это неправильный подход. Если вы хотите, чтобы приобретенный агрегат был полезен в тренировках, а не использовался как вешалка для одежды, тогда обратите внимание на следующие моменты:
- Рост и вес. Чтобы определиться с максимально допустимым весом пользователя, прибавьте к своей массе 15-20 кг. Что касается роста, то здесь лучше всего опробовать приобретаемый тренажер прямо в магазине. Кому-то будет достаточно маленькой модели с шагом 30 см, а кому-то лучше купить более крупный тренажер с шагом 50 см.
- Цена тренажера эллипсоид. Данный параметр обычно является самым важным при покупке. На формирование стоимости влияет следующее: тип торможения, дополнительные функции, производитель и габариты тренажера.
- Занимаемое пространство. Как правило, не у всех в квартире или доме есть много свободного места для установки больших тренажеров, поэтому продумайте сразу, где будет стоять ваш орбитрек, и измерьте пространство – подобным образом можно узнать нужные габариты устройства.
- Тип нагрузки на маховик. При классификации по данному критерию различают такие модели, как механическая, магнитная и электромагнитная.
Постарайтесь учесть все вышеперечисленные моменты, а уже потом обращайте внимание на фото тренажера эллипс, так как для некоторых внешний вид устройства все-таки тоже важен.
Если говорить о цене орбитрека, то на ее формирование существенно влияет тип торможения, поэтому давайте рассмотрим все существующие варианты:
- Механический. Этот вид уже не пользуется популярностью ни у производителей, ни у покупателей. Такие тренажеры очень шумные и не могут обеспечить нормальную плавность хода, хотя это один из самых важных показателей для орбитреков. Механические модели являются представителями дешевого ценового сегмента.
- Магнитный. Эти тренажеры имеют средние цены, достаточно плавный ход, низкий уровень шума. Однако для увеличения нагрузки вам придется все время сходить с эллипса и крутить специальный механический переключатель.
- Электромагнитный. Такие модели являются самыми дорогими, но при этом они более комфортабельны, функциональны и точны в измерениях показателей. Почти во всех электромагнитных тренажерах есть бортовой компьютер, с помощью которого возможно увеличить нагрузку, не сходя с устройства, или запустить программу тренировки.
Цены, характеристики, список дополнительных опций и фотографии тренажеров эллипсоидов – все это можно найти в карточках товаров нашего интернет-магазина. Помните, что купить эллиптический тренажер в интернете намного проще и дешевле.
По всем вопросам, касающимся товаров магазина «Зона Спорта», звоните на номер 8-800-333-47-80 (звонок бесплатный с любого номера в РФ).
Эллипсоид вращения — Википедия
Материал из Википедии — свободной энциклопедии
 Сфера — нормальный сфероид
Сфера — нормальный сфероид  Вытянутый сфероид
Сплюснутый сфероид
Вытянутый сфероид
Сплюснутый сфероидЭллипсо́ид враще́ния (сферо́ид) — поверхность вращения в трёхмерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей.
Термин «сфероид» для обозначения двух вариантов эллипсоида вращения ввёл Архимед: «… мы полагаем следующее: если эллипс при сохранении неподвижной большей оси поворачивается, возвращаясь в исходное положение, то охватываемая им фигура будет называться вытянутым сфероидом (παραμακες σφαιροιδες). Если эллипс поворачивается при сохранении в неподвижности малой оси и возвращается назад, то охватываемая им фигура будет называться сплюснутым сфероидом (επιπλατυ σφαιροιδες).» [1]
Эллипсоид вращения является частным случаем эллипсоида, две из трёх полуосей которого имеют одинаковую длину (ax=ay=a{\displaystyle a_{x}=a_{y}=a}):
- x2ax2+y2ay2+z2b2=ρ2a2+z2b2=1.{\displaystyle {\frac {x^{2}}{{a_{x}}^{2}}}+{\frac {y^{2}}{{a_{y}}^{2}}}+{\frac {z^{2}}{b^{2}}}={\frac {\rho ^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1.}
В частном случае, когда все три полуоси равны, исходный эллипс представляет собой окружность, а эллипсоид вращения вырождается в сферу.
Вытянутый эллипсоид вращения (вытянутый сфероид) можно также определить как геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек (фокусов) постоянна.
Зеркало в виде вытянутого эллипсоида вращения обладает следующим свойством: лучи света, исходящие из одного из фокусов эллипсоида, после отражения соберутся в другом фокусе.
Сплюснутый эллипсоид вращения (сплюснутый сфероид) можно также определить как геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна.
- Площадь поверхности:
- 2πa(a+b2a2−b2ln(a+a2−b2b)){\displaystyle 2\pi a\left(a+{\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}\ln \left({\frac {a+{\sqrt {a^{2}-b^{2}}}}{b}}\right)\right)}, (для сплюснутого, a > b)
- 2πa(a+b2b2−a2arcsin(b2−a2b)){\displaystyle 2\pi a\left(a+{\frac {b^{2}}{\sqrt {b^{2}-a^{2}}}}\arcsin \left({\frac {\sqrt {b^{2}-a^{2}}}{b}}\right)\right)}, (для вытянутого, a < b)
- 43πa2b{\displaystyle {\frac {4}{3}}\pi a^{2}b}
Здесь oε{\displaystyle o\!\varepsilon } — угловой эксцентриситет:
- oε=arccos(ba)=2arctan(a−ba+b){\displaystyle o\!\varepsilon =\arccos \left({\frac {b}{a}}\right)=2\arctan \left({\sqrt {\frac {a-b}{a+b}}}\right)\quad \mathrm {} }, (сплюснутый)
- =arccos(ab)=2arctan(b−ab+a){\displaystyle =\arccos \left({\frac {a}{b}}\right)=2\arctan \left({\sqrt {\frac {b-a}{b+a}}}\right)\quad \mathrm {} }, (вытянутый)
- oε=arccos(ba)=2arctan(a−ba+b){\displaystyle o\!\varepsilon =\arccos \left({\frac {b}{a}}\right)=2\arctan \left({\sqrt {\frac {a-b}{a+b}}}\right)\quad \mathrm {} }, (сплюснутый)
- (sin(oε) часто выражается как эксцентриситет, «e»)
Форма Земли — в хорошем приближении представляет собой сплюснутый эллипсоид вращения с ab≈301299{\displaystyle {{\frac {a}{b}}\approx {\frac {301}{299}}}}.
Свойство вытянутого эллипсоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Грегори и в антеннах Грегори.
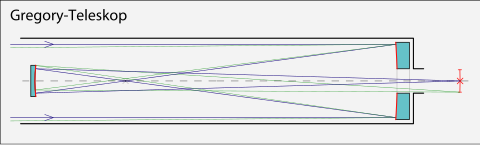 | ||||||||||
| Слева — радиотелескоп РТ-70, исполненный по системе антенны Грегори. Справа — оптическая схема телескопа Грегори; малое зеркало имеет форму вытянутого эллипсоида вращения | ||||||||||
- ↑ L. Russo. The forgotten revolution (неопр.). — Springer, Berlin, 2004. — С. 180.
Эллипсоид
Эллипсоид (рис.7) (от «эллипс»
и греч. «eidos» — вид) — замкнутая
центральная поверхность
второго порядка. Эллипсоид имеет
центр симметрии – 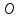 и три оси симметрии, которые называются
осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
и три оси симметрии, которые называются
осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
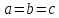 —
сфера.
—
сфера.
В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
Форма эллипсоида.
Исследуем
форму эллипсоида. Из уравнения 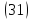 видно, что координаты точек поверхности
ограничены:
видно, что координаты точек поверхности
ограничены:
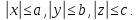
Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат.
Для
выяснения формы эллипсоида рассмотрим
его сечения плоскостями. Найдем линию
пересечения эллипсоида с плоскостью 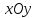 .
Так как любая точка плоскости
.
Так как любая точка плоскости имеет
нулевую третью координату,
имеет
нулевую третью координату,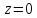 ,
то координаты точек эллипсоида на
плоскости
,
то координаты точек эллипсоида на
плоскости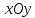 удовлетворяют
уравнению:
удовлетворяют
уравнению:
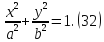
Получаем,
что линия пересечения является эллипсом
с полуосями 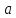 и
и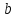


Рис.
8.
Сечение
плоскостью 
Аналогично,
сечение в плоскости 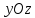 ,
дает эллипс:
,
дает эллипс:
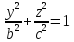
с
полуосями 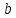 и
и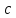 ,
а сечение плоскостью
,
а сечение плоскостью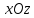 – эллипс:
– эллипс:
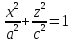
с
полуосями 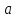 и
и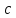
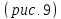
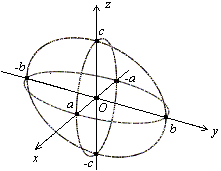
Рис.9. Сечения эллипсоида координатными плоскостями
Нарисованный
«каркас» из сечений уже дает
представление об эллипсоиде. Но чтобы
выяснить, как ведет себя поверхность
между нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью 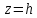 .
Эта плоскость параллельна плоскости
.
Эта плоскость параллельна плоскости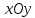 и
пересекает ось
и
пересекает ось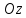 в
точке
в
точке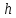 .
Уравнения этой линии:
.
Уравнения этой линии:
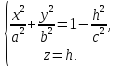
Очевидно,
что если 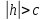 ,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой —
отрицательное.
,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой —
отрицательное.
Если 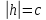 ,
то в сечении получим лишь одну точку
,
то в сечении получим лишь одну точку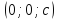 или
или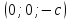 в
зависимости от знака
в
зависимости от знака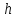 .
.
Пусть 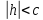 .
Тогда первое уравнение преобразуем к
виду:
.
Тогда первое уравнение преобразуем к
виду:
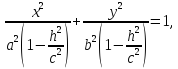
то есть к виду:
где 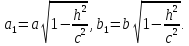
Уравнение 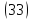 является уравнением эллипса, подобного
эллипсу, задаваемому уравнением
является уравнением эллипса, подобного
эллипсу, задаваемому уравнением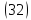 ,
с коэффициентом подобия
,
с коэффициентом подобия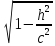 и
полуосями
и
полуосями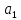 и
и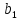 .
Ясно, что сечение плоскостью
.
Ясно, что сечение плоскостью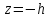 является
таким же эллипсом, расположенным
симметрично первому относительно
плоскости
является
таким же эллипсом, расположенным
симметрично первому относительно
плоскости .
Нарисуем эти сечения
.
Нарисуем эти сечения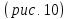 .
.
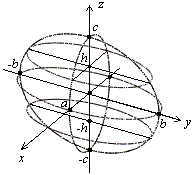
Рис.10. Дополнительные сечения эллипсоида
Таким
образом, весь эллипсоид составлен из
эллипсов, лежащих в плоскостях,
параллельных плоскости 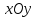 и
подобных эллипсу в плоскости
и
подобных эллипсу в плоскости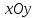 .
.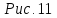 дает более привычное глазу изображение
эллипсоида:
дает более привычное глазу изображение
эллипсоида:
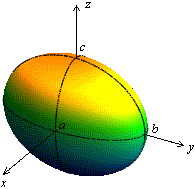
Рис.11. Эллипсоид
Так
же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии — центром эллипсоида. Числа 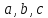 называются
полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
называются
полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
Если
две полуоси равны друг другу, то эллипсоид
называется эллипсоидом вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если 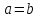 ,
то все сечения эллипсоида плоскостями
,
то все сечения эллипсоида плоскостями
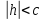 ,
будут окружностями. Сам эллипсоид может
быть получен из эллипса:
,
будут окружностями. Сам эллипсоид может
быть получен из эллипса:

лежащего
в плоскости 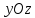 ,
при вращении его вокруг оси
,
при вращении его вокруг оси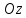
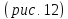 .
.

Рис.12. Эллипсоид вращения
Эллипсоид — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2017; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2017; проверки требуют 2 правки.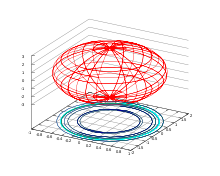 Эллипсоид вращения
Эллипсоид вращенияЭллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:
- x2a2+y2b2+z2c2=1,{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1,} где a,b,c{\displaystyle a,b,c} — произвольные положительные числа.
Величины a, b, c называют полуосями эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.
В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.
Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли.
Параметрическое уравнение эллипсоида
- x=asin(θ)cos(φ),y=bsin(θ)sin(φ),z=ccos(θ),{\displaystyle {\begin{aligned}x&=a\sin(\theta )\cos(\varphi ),\\y&=b\sin(\theta )\sin(\varphi ),\\z&=c\cos(\theta ),\end{aligned}}\,\!}
где
- 0≤θ≤π,0≤φ<2π.{\displaystyle 0\leq \theta \leq \pi ,\qquad 0\leq \varphi <2\pi .}
Площадь поверхности эллипсоида вращения[источник не указан 2381 день]:
- S=4πb2(1+23e2+35e4+47e6+…+k+12k+1e2k+…).{\displaystyle S=4\pi b^{2}\left(1+{\frac {2}{3}}e^{2}+{\frac {3}{5}}e^{4}+{\frac {4}{7}}e^{6}+…+{\frac {k+1}{2k+1}}e^{2k}+…\right).}
В элементарных функциях[источник не указан 2381 день]:
- Soblate=2πa2(1+1−e2earthe),e2=1−c2a2(c<a),{\displaystyle S_{\rm {oblate}}=2\pi a^{2}\left(1+{\frac {1-e^{2}}{e}}\mathrm {arth} \,e\right)\quad {\mbox{,}}\quad e^{2}=1-{\frac {c^{2}}{a^{2}}}\quad (c<a),}
- Sprolate=2πa2(1+caesin−1e),e2=1−a2c2(c>a),{\displaystyle S_{\rm {prolate}}=2\pi a^{2}\left(1+{\frac {c}{ae}}\sin ^{-1}e\right)\quad \qquad {\mbox{,}}\;\quad e^{2}=1-{\frac {a^{2}}{c^{2}}}\quad (c>a),}
Oblate, prolate — сплюснутый и вытянутый соответственно.
Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Объём эллипсоида:
- V=43πabc.{\displaystyle V={\frac {4}{3}}\pi abc.}
 Вытянутый эллипсоид вращения Вытянутый эллипсоид вращения | Сплюснутый эллипсоид вращения | Сплюснутый эллипсоид вращения и его образующая |  Трехосный эллипсоид с различными длинами полуосей Трехосный эллипсоид с различными длинами полуосей |
что общего, в чём отличие эллипса от овала
В школе большинству из нас не раз объясняли, в чём отличие радиуса от диаметра, серной кислоты от соляной, эллипса от овала. Но прошли годы, и школьные знания, «слежавшись» под весом многолетней будничной рутины, по большей части позабылись. В рамках данной статьи мы попытаемся восполнить хотя бы один досадный пробел в знаниях и подробнее рассмотрим последний из приведённых примеров, научившись отличать овал от эллипса. Для начала обозначим ключевые определения.
Овал
Под овалом в геометрии понимается вытянутая замкнутая фигура правильной формы. Овал относится к двухмерным фигурам и обладает особыми свойствами. Само слово образовано от французского Ovale, которое, в свою очередь, имеет общие корни с латинской лексемой ovum, что в переводе означает «яйцо». Кривая этого геометрического объекта имеет с любой прямой не более двух общих точек.
Справка! Нельзя сказать, что человек, называющий данную геометрическую фигуру просто «кругом», абсолютно прав. На самом деле окружность (в которой, как мы знаем, все точки кривой равноудалены от центра) – это одна из множества вариаций овала.
Существует структурно более сложное понятие овала в инженерной графике. В этой отрасли науки данным термином обозначают фигуру, имеющую две оси симметрии и построенную при помощи сочетания четырёх участков кривых линий от двух радиусов. Эти участки подобраны таким образом, чтобы обеспечить «перетекание» от одного радиуса к другому без нарушения симметрии и контура фигуры. Если определять координаты точки, постоянно движущейся по линии овала, то она всегда будет находиться на одном из вышеописанных радиусов кривизны. Эти радиусы считаются «фиксированными».
Эллипс
У слова «эллипс» имеются греческие корни, наиболее близкие по переводу к словам «нехватка, недостаток, опущение». Чего же не хватает в эллипсе и что эта фигура вообще из себя представляет?
Эллипсом принято считать любую замкнутую кривую на плоскости, которая имеет четыре вершины в так называемых точках экстремума. Точки фокуса эллипса равноудалены от его вершин. Стороны эллипса будут симметричны, если разделить его в любом направлении прямой, проходящей через его центр. Впрочем, это правило действительно и для фигур овального типа.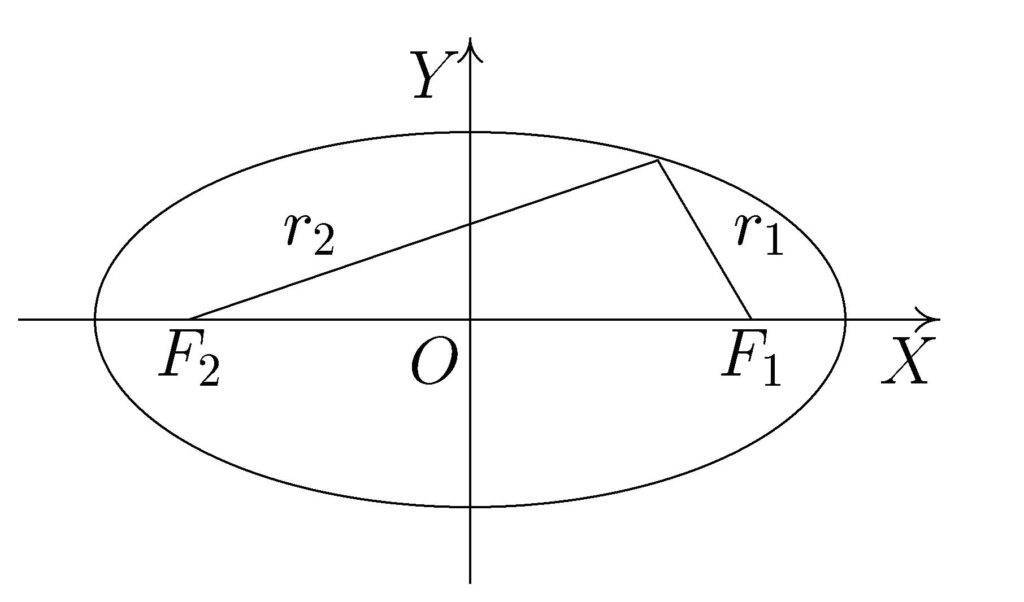
Что общего
Рассматривая вопрос о том, что может быть общего между овальной и эллиптической фигурой, можно заключить, что они имеют весьма похожий внешний вид. Кроме того, обе фигуры располагаются в так называемом евклидовом пространстве. На простом языке евклидово пространство можно объяснить как двумерное пространство, в котором положение точки может быть обозначено при помощи двух чисел, обозначающей её координаты.
В чём отличие эллипса от овала
Различия между двумя этими весьма смежными понятиями вытекают в основном из их определений. Вернувшись к рассмотренному нами определению овала в инженерной графике, можно заключить, что он, в отличие от эллипса, в котором радиус кривизны варьируется перманентно, обладает «фиксированными» радиусами.
Справка! В трёхмерном пространстве возможно построение объёмного овала. Такие фигуры называются эллипсоидами и способны иметь приплюснутую или вытянутую форму. Эта форма достаточно широко распространена в макромире: ею обладает огромное количество известных планет и даже галактики.
Для овальных фигур существует великое множество вариантов построения. Оси их, начинающиеся в точках своих вершин, имеют различные соотношения между собой. В случае же с эллиптическими фигурами в силу вступают особые правила построения. Говоря проще, овалом обозначают более общее понятие, а эллипсом – лишь одно из его проявлений.
Эллипс. Полуоси эллипса. Фокус эллипса.
Эллипс- замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. На рисунке ниже показано несколько примеров.
Круг-это частный случай эллипса, который получается, когда сечение через конус или цилиндр ортогонально оси конуса или цилиндра.

Эллипс-это фигура, в результате сечения конуса и прямого кругового цилиндра
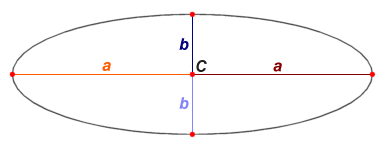
Эллипс симметричен относительно горизонтальной и вертикальной осей, как показано на рисунке выше. Максимальное расстояние между двумя точками происходит вдоль горизонтальной оси (называемой главной осью или поперечным диаметром), а минимальное расстояние между двумя точками-вдоль вертикальной оси (называемой малой осью или сопряженным диаметром). Антиподальные точки — это любые две точки по периметру эллипса, так что соединяющий их отрезок линии должен проходить через центр с эллипса (что происходит на пересечении горизонтальной и вертикальной осей). Эллипс симметричен относительно его большой и малой осей.
Полуось — это та часть оси, которая лежит между центром \(C\) и периметром эллипса — называется полуосью. Полуоси, принадлежащие к главной оси — большая полуось, а полуось, принадлежащих к малой оси — малая полуось. На приведенной выше рисунке мы обозначили каждую из двух полуосей \(a\) и каждую из двух полуосей \(b\). Точки, показанные красным цветом по периметру эллипса, являются точками, где большая и малая оси пересекают периметр эллипса. Это вершины эллипса. Вершины — это точки, в которых кривизна эллипса максимальна (т. е. где главная ось пересекает периметр эллипса).
Есть две специальные точки, которые лежат на главной оси эллипса, равноудаленной от его центра C, каждая из которых является фокусом эллипса. Эти две точки (совместно называемые фокусами эллипса) обычно обозначаются как \(F1\) и \(F2\). Расположение фокусов таково, что для любой точки \(p\) по периметру эллипса сумма расстояний от \(F1\) до \(P\) и от \(F2\) до \(P\) остается постоянной и будет равна длине главной оси. Фактически, принимая любую произвольную пару точек в качестве фокусов и любое значение длины главной оси, которое больше расстояния между этими двумя точками, соответствующий эллипс определяется как набор точек, для которых сумма расстояний между точкой и каждым из фокусов равна длине главной оси.
Сумма расстояний от фокусов до любой точки эллипса есть постоянная
Расстояние между любым из фокусов и центром эллипса называется фокусным расстоянием и будет зависеть от длины главной и малой осей. Мы обозначили отрезки линии, соединяющие каждый фокус с центром эллипса \(C\). Длину\( c\) (т. е. Фокусное расстояние) можно найти по следующей формуле:
\(с= \sqrt{a^2-b^2} \)
где \(a\) и \(b\)-длины главной и малой осей соответственно. Обратите внимание, что чем дальше фокусы от центра эллипса, тем меньше сходство между эллипсом и окружностью. Кривизна в вершинах эллипса будет увеличиваться, в то время как кривизна в \(cо\)-вершинах будет уменьшаться. Другими словами, эллипс станет более плоским по мере увеличения значения \(c\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!

Добавить комментарий